Inklusiver Unterricht zur elementaren Algebra
Ein wichtiger Themenbereich der Sekundarstufe I ist die elementare Algebra. Mit ihrer Hilfe ist es möglich, „Zusammenhänge zwischen Zahlen allgemein durch Terme und Gleichungen zu beschreiben und damit Probleme allgemein zu lösen. Solche Probleme können in der realen Welt, aber auch in der Mathematik aufkommen“ (Barzel, Glade & Klinger, 2021, S. 2). Daher ist es für alle SchülerInnen des inklusiven Mathematikunterrichts relevant, Ansätze für die Lösung solcher Probleme kennenzulernen und zu verstehen. Dies ist auch in den Kernlehrplänen des Landes NRW verankert, in denen insbesondere die Relevanz des problemlösenden Arbeitens in inner- und außermathematischen Kontexten hervorgehoben wird (QUA-LiS NRW, 2023).
Zur allgemeinen Lösung von Problemen in der elementaren Algebra sind zwei übergeordnete Tätigkeiten von besonderer Bedeutung (vgl. Barzel, Glade & Klinger, 2021):
- Das kalkülmäßige Operieren im Sinne einer regelgeleiteten Veränderung formal-symbolischer Darstellungen und
- das inhaltliche Denken in Bildern oder Situationen, bei dem über die Bedeutung symbolisch-algebraischer Darstellung nachgedacht wird.
Diese beiden Tätigkeiten müssen im inklusiven Mathematikunterricht miteinander vernetzt werden. Dabei plädiert Prediger (2009) für die Vermittlung des inhaltlichen Denkens vor dem kalkülmäßigen Operieren, „weil ein Kalkül ohne inhaltliche Grundlage für die Anwendung von Mathematik bedeutungslos ist“ (ebd. S. 10). Doch welche inhaltlichen Grundlagen sind in der elementaren Algebra für das Kalkül relevant?
Hier ist zunächst das Variablenkonzept zu nennen. Es ist besonders wichtig, da die Deutung von Variablen die Konzepte von Termen und Gleichungen unmittelbar beeinflusst und da diese Konzepte für die allgemeine Lösung von Problemen in der elementaren Algebra von Bedeutung sind (vgl. Korntreff & Prediger, 2021). In der mathematikdidaktischen Literatur wurden schon viele Deutungen der Variable unterschieden und für Terme und Gleichungen entsprechend abgeleitet (vgl. z. B. Malle, 1993). Die folgende Tabelle integriert einige dieser Deutungen und bietet eine Übersicht über die verschiedenen Konzepte von Variablen (1) und die darauf basierenden Deutungen von Termen (2) und Termgleichwertigkeit (3) sowie Deutungen von Gleichungen (4) und Gleichungsäquivalenz (5):
| 1 | Einsatzstelle für Zahlen | Unbekannte, gesuchte Zahl | Zahlen, für die man verallgemeinert | Veränderliche Größe | Ungedeutetes Symbol (Kalkül) |
| 2 | Rechen-vorschrift, in die Zahlen eingesetzt werden können | Beschreibung für weitere Unbekannte | Allgemeine Beschreibung… | Ungedeutete Symbolkette | |
| …eines Zusammen-hangs | …eines funktionalen Zusammen-hangs | ||||
| 3 | Einsetzungs-gleichheit: 2 Terme ergeben für alle Einsetzungen denselben Wert | – | Beschreibungsgleichheit: 2 Terme beschreiben… | Umformungs-gleichheit: 1. Term in 2. Term regelgeleitet überführbar | |
| …dasselbe (Bild, Situation…) | …einen funktionalen Zusammenhang | ||||
| 4 | Aussageform zur Prüfung potenzieller Lösungen durch Einsetzen | Bestimmungs-gleichung als Bedingung zur Ermittlung der Unbekannten | Allgemeingültige Bedingung für | Ungedeutete Symbolkette | |
| alle Zahlen | einen funktionalen Zusammenhang | ||||
| 5 | 2 Gleichungen mit derselben Lösungs-menge | 2 Gleichungen beschreiben dieselben Unbekannten | – | – | 1. Gleichung in 2. Gleichung regelgeleitet überführbar |
Zwei Spalten dieser Tabelle sollen nun exemplarisch beleuchtet werden. Die Variable kann zum Beispiel als Einsatzstelle für Zahlen begriffen werden, was die Deutung eines Terms als Rechenvorschrift nahelegt, in die Zahlen eingesetzt werden können. Diese Deutung hat wiederum zur Folge, dass eine Gleichung als Aussageform interpretiert wird, welche unterschiedliche, von der Einsetzung abhängige Wahrheitswerte besitzt (vgl. Korntreff & Prediger, 2021). Die folgende Aufgabe aus dem Smart-Test illustriert ein solches Verständnis von Variablen, Termen und Gleichungen:

Ein anderes Beispiel für eine Deutung der Variable ist die der unbekannten Zahl: „Wird die Variable als unbekannte Zahl gedeutet, so ist der Term eine Beschreibung für eine weitere, unbekannte Zahl, bspw. (x+y)/2 das unbekannte arithmetische Mittel von x und y, das nun gleichgesetzt werden kann mit einem vorgegeben Wert“ (Korntreff & Prediger, 2021, S. 288). Damit wird die Gleichung zu einer „Bestimmungsgleichung“ (ebd., S. 290), mit der die unbekannte Zahl ermittelt werden soll. Für die Ermittlung der unbekannten Zahl ist die Umformung der gegebenen Terme von Nöten. Um diese Tätigkeit zu verstehen, ist eine Auseinandersetzung mit den Konzepten der Termgleichwertigkeit und Gleichungsäquivalenz von Bedeutung. Diese beiden Konzepte werden ebenfalls von dem der Variablen bestimmt. So lässt sich beispielsweise die Termgleichwertigkeit bei der Deutung von Variablen als Einsatzstellen für Zahlen als
Einsetzungsgleichheit verstehen, d. h.: „Zwei Terme sind dann gleichwertig, wenn sie für alle eingesetzten Zahlen denselben Wert ergeben“ (ebd. S. 290). Entsprechend wird die Gleichungsäquivalenz so gedeutet, dass zwei Gleichungen dieselbe Lösungsmenge haben. Für die Variable als unbekannte Zahl ist die Deutung der Gleichungsäquivalenz etwas anders: Hier versteht man unter dem Begriff, dass zwei Gleichungen dieselben Unbekannten beschreiben (vgl. ebd.).
Aufgrund der Tragweite des Variablenkonzepts ist es von besonderer Bedeutung, dass alle SchülerInnen im inklusiven Mathematikunterricht vielfältige Erfahrungen mit Variablen machen, um die verschiedenen Deutungen und darauf aufbauende Konzepte begreifen zu können. Dabei gilt weiterhin der Grundsatz des inhaltlichen Denkens vor dem Kalkül – insbesondere bei Rechenschwierigkeiten (vgl. Prediger, 2009). Doch wie lässt sich dies in der Sekundarstufe konkret umsetzen?
Ein Beispiel dafür liefern Korntreff und Prediger (2022) in ihrer Unterrichtseinheit Zusammenhänge allgemein beschreiben mit Variablen und Termen , welche die Variable als Veränderliche und als Unbekannte fokussiert. Darin werden sukzessiv die folgenden Kompetenzen aufgebaut:
- Variablen situationsangemessen deuten und verschiedene Deutungen kontrastieren.
- Terme und Gleichungen als Beziehungen zwischen Größen im Sachkontext interpretieren, Terme als Beschreibungsmittel und Gleichungen als Bedingung nutzen.
- Darstellungen interpretieren und verknüpfen (vgl. ebd. S. 3)
Um die Variable als Veränderliche und den Term als Beziehung zwischen Größen zu deuten, wurde beispielsweise die folgende Aufgabe gewählt:
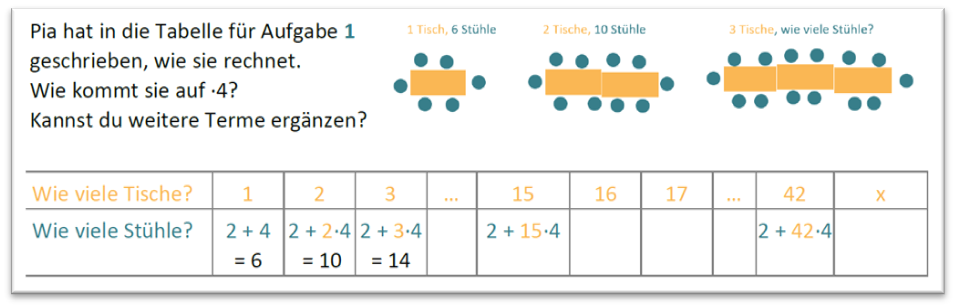
Diese Aufgabe kann von Lernenden auf unterschiedlichen Niveaus bearbeitet werden. So ist es beispielsweise möglich, auf verschiedene Darstellungsebenen zurückzugreifen und zwischen diesen Darstellungen hin und her zu wechseln (vgl. z. B. Bruner, 1970). Alternativ können verschiedene Zahlbereiche thematisiert werden, bevor die Variable als Veränderliche selbst eingeführt wird. Zudem stehen für diese und weitere Aufgaben sprachliche Impulse zur Verfügung, mit denen Lernende mit besonderen Bedürfnissen unterstützt werden können (vgl. Korntreff & Prediger, 2022). Die Konzepte der Variablen, Terme und Gleichungen können insgesamt als fundamentale Ideen der Algebra charakterisiert werden: Sie sind nicht auf bestimmte Jahrgangsstufen und auch nicht auf bestimmte intellektuelle Stufen bezogen. Stattdessen können sie auf unterschiedlichen Niveaus vermittelt werden. Schon in der Grundschule und in der Sekundarstufe I wird propädeutisch strukturorientierte Arithmetik betrieben: Immer wieder werden dort „typische algebraische Denkhandlungen wie das beziehungsreiche Strukturieren von Situationen und graphischen Darstellungen (z. B. Plättchenmustern), Zahlentermen und Gleichungen (4+_=5+_) und das Verallgemeinern“ vollzogen, und in Zahlenrätseln wird „das Rückwärtsrechnen und das Finden unbekannter Werte“ thematisiert (Barzel, Glade & Klinger, 2021, S. 45). In allen Jahrgangsstufen werden diese Ansätze dann im Sinne des Spiralprinzips (Bruner, 1970) immer wieder in strukturell angereicherter Form aufgegriffen und auf einem höheren Niveau mit neuen Vorstellungen und Fertigkeiten z. B. im Umgang mit Funktionen verknüpft. Dabei erkunden und vertiefen die SchülerInnen den algebraischen Themenkomplex in Abhängigkeit von ihren individuellen Lernvoraussetzungen in unterschiedlicher Breite und Tiefe. Auf diese Weise können SchülerInnen aller Leistungsniveaus am inklusiven Mathematikunterricht teilhaben.
