Gemeinsames Lernen am gemeinsamen Gegenstand
Diese Lernsituation wird vielfach als ein Ideal des inklusiven Mathematikunterrichts angesehen. Wird ein der fundamentalen Idee zugrundeliegender und konstituierender Aspekt, also ein struktureller Kern der Idee, gemäß des Spiralprinzips derart ausdifferenziert, dass der strukturelle Kern auf mehreren Niveaus bearbeitet werden kann, erhält man einen gemeinsamen Gegenstand. Dementsprechend arbeiten alle Schülerinnen und Schüler einer Lerngruppe nicht neben-, sondern miteinander an denselben mathematischen Prozessen und Phänomenen, jedoch auf unterschiedlichen Bearbeitungsniveaus. Dazu wird ein vielschichtiger, aber logisch zusammenhängender Themenkomplex benötigt, damit die Lernenden auf mehreren, unterschiedlichen Bearbeitungsniveaus arbeiten können. Dieser gemeinsame Gegenstand ermöglicht dabei jedem Lernenden an eigenen Zielsetzungen zu arbeiten und im Rahmen kooperativer Prozesse im Sinne eines von- und miteinander Lernens neue Erkenntnisse zu generieren. Dies bedeutet, dass manche Lernende erste Erfahrungen mit dem Unterrichtsgegenstand machen, während andere schon zugrundeliegende, vertiefende Zusammenhänge erkennen und begründen. Durch die Implementierung eines gemeinsamen Gegenstandes kann ein fachlicher Austausch über den gemeinsamen strukturellen Kern, mit dem sich alle Schülerinnen und Schüler auf verschiedenen Niveaus beschäftigen, initiiert werden, sodass die individuellen Lernprozesse gemeinsam und nicht nur gleichzeitig erfolgen, also alle Schülerinnen und Schüler wirklich gemeinsam lernen.
Beispiel: Im Rahmen des inklusiven Mathematikunterrichts kann die Notation von Zahlen in verschiedenen Zahldarstellungen und der flexible Darstellungswechsel zwischen den Zahlrepräsentationen den gemeinsamen Gegenstand bilden, um den herum die Lernenden auf verschiedenen Niveaus arbeiten. Dieser gemeinsame Gegenstand ist ein wichtiger Aspekt zur Förderung des dezimalen Stellenwertverständnisses (fundamentale Idee des Dezimalsystems) und stellt gleichzeitig eine kritische Stelle im Lernprozess dar (Häsel-Weide & Nührenbörger 2013).
In der 6. Klasse könnten durch den Einsatz struktur-analoger Aufgaben manche Lernende im Bereich der natürlichen Zahlen arbeiten und andere im Bereich der Dezimalbrüche (s. Abb.). Struktur-analoge Aufgaben ermöglichen im Sinne einer inneren Differenzierung eine Bearbeitung auf unterschiedlichen Niveaus entlang des gemeinsamen Gegenstandes. Die Schülerinnen und Schüler erhalten alle die gleiche Aufgabe: verschiedene Zahlen, die durch das Legen von Plättchen in die Stellenwerttafel entstehen sowohl als additive Zerlegung als auch in der formal-symbolischen Schreibweise darzustellen; allerdings operieren sie dabei in unterschiedlichen Zahlenräumen.
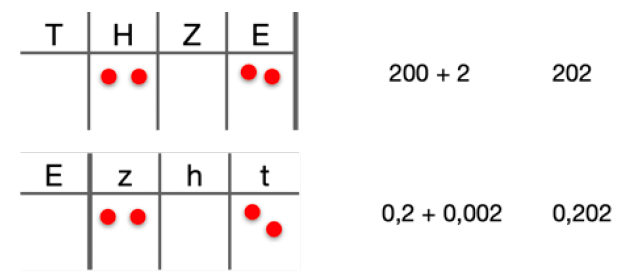
Im Unterricht kann die Auseinandersetzung mit dem gemeinsamen Gegenstand unter anderem auf zwei Arten erfolgen: Zum einen könnten alle Lernenden durchgehend kooperativ in aufeinander bezogenen Rollen an dem gemeinsamen Gegenstand arbeiten (kooperatives Setting der Wippe; Häsel-Weide et al. 2019) und dabei sich gegenseitig die Plättchen in die Stellenwerttafel legen und dadurch für die Partnerin bzw. den Partner die Zahlen generieren; anschließend müssten die entstandenen Zahlen in den verschiedenen Zahlrepräsentationen dargestellt werden. Die Tätigkeiten begleitend sollten die Lernenden ihr Vorgehen beschreiben; gleichzeitig sollte die bzw. der Lernende, welche(r) die Plättchen in die Stellenwerttafel gelegt hat, die Ergebnisse kontrollieren. Auf diese Weise könnten beide Lernende sich über das gemeinsame Arbeiten austauschen.
Zum anderen wäre es möglich, dass zunächst in einer Einzelarbeitsphase die Lernenden Zahlen in verschiedenen Notationsformen darstellen, allerdings operieren sie dabei in unterschiedlichen Zahlbereichen. Im Anschluss erfolgt eine Partnerarbeit (kooperatives Setting der Weggabelung; Häsel-Weide et al. 2019). Unabhängig von der genauen Vorgehensweise ist es wichtig, dass sich die Lernenden über die zugrundeliegenden mathematischen Strukturen des gemeinsamen Gegenstandes austauschen können; gegebenenfalls muss dies durch konkrete weiterführende Aufgaben oder Impulse initiiert werden. So wäre es in dem Beispiel sinnvoll, auf multiplikative dezimale Beziehungen zwischen Stellenwerten, Veränderungen der Werte einzelner Stellenwerte durch Verschieben eines oder mehrerer Plättchen, die Bedeutung der Null als Platzhalter unbesetzter Stellen oder Gemeinsamkeiten bzw. Unterschiede zwischen natürlichen Zahlen und Dezimalbrüchen einzugehen.
Bei der Kooperation an einem gemeinsamen Gegenstand fokussieren sich alle Schülerinnen und Schüler auf eine gemeinsame Idee, also auf einen Aspekt des gemeinsamen Gegenstandes, zu dem alle einen Zugang erhalten sollen und der zusammen ausgehandelt wird. Damit wird die fachliche Vielfalt an unterschiedlichen mathematischen Aspekten, die bei der Beschäftigung mit einem mathematischen Gegenstand möglich wären, auf einen gemeinsamen strukturellen Kern begrenzt. Die individuellen Lernziele beziehen sich zwar auf die gemeinsame Idee, weisen jedoch zieldifferente Ausprägungen auf (vgl. Abb.).
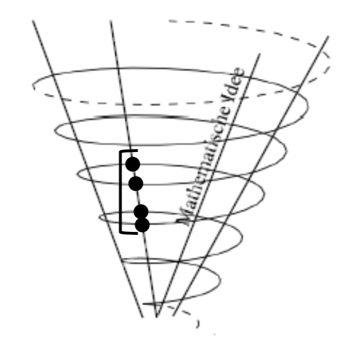
Besonders für den inklusiven Mathematikunterricht besteht durch die große Vielfalt an unterschiedlichen Kompetenzen und Lernvoraussetzungen die Hoffnung, dass dies zu einer breiten Spanne an mathematischen Vorstellungen, Vorgehensweisen und Deutungen führt und die Schülerinnen und Schüler im Rahmen einer Kooperation von den Beiträgen ihrer Mitlernenden profitieren können. Allerdings muss beachtet werden, dass die Spanne der individuellen Kompetenzen, die in ihrer Heterogenität produktiv wirken können, nicht zu groß werden darf. Beim Austausch muss die gemeinsame Kernidee im Vordergrund stehen. Sind die Unterschiede jedoch zu groß, besteht die Gefahr, dass die Lernenden sich gar nicht oder nur oberflächlich austauschen.
